Causal Inference for Genetic Associations
Published:
Recently I’ve become interested in causal inference, as I’ve been exploring both the foundational approaches and the more recent applications to machine learning. An important application is genome-wide association studies (GWAS), where biologists attempt to uncover the causal link between genotypes and traits of interest (i.e. what part of the genome causes orange hair?).
In this post, I’ll go over one specific GWAS approach by Minsun Song, Wei Hao, and John Storey, as described in “Testing for genetic associations in arbitrarily structured populations.” Although their writeup is specific to genetic studies, the main ideas of the paper extend to applications beyond GWAS. No background in genetics is required for this summary.
The Genotype-Conditional Association Test
We’re interested in testing whether certain genes cause a trait, but there are two confounding problems:
- Genotype frequencies aren’t homogeneous – specific and complicated population patterns are encoded into the genome (these may also affect the trait of interest). In statistical terms, I think this amounts to the genotypes not being i.i.d.
- There may be non-genetic factors that affect the trait of interest, such as lifestyle or environment.
Song et. al’s solution to this problem is, in my opinion, the coolest thing about the paper: they introduce a latent catch-all variable, \(z\), which captures information including population structure (which directly affects the genotype frequencies) and non-genetic factors (which directly affect the the trait of interest).
First, some notation (I’m diverging slightly from the notation used in the paper): we have \(n\) human beings, and for each human \(i\), we are interested in a particular trait of interest \(y_i\). Each human has \(m\) SNP’s, referred to as \(x_{ij} \in \{0,1,2\}\) for human \(i\) and SNP \(j \in 1, \dots, m.\) In the causal inference framework, each \(x_{ij}\) is a treatment, and we would like to know which are causally linked to the outcome \(y_i\) (which I’ll assume is continuous for this post). SNP’s refer to specific genome locations, and the \(x_{ij}\) values refer to the possible pairs of letters the alleles can take on. Introducing \(z_i\), the diagram below (modified from the original paper) depicts the relationships of interest:
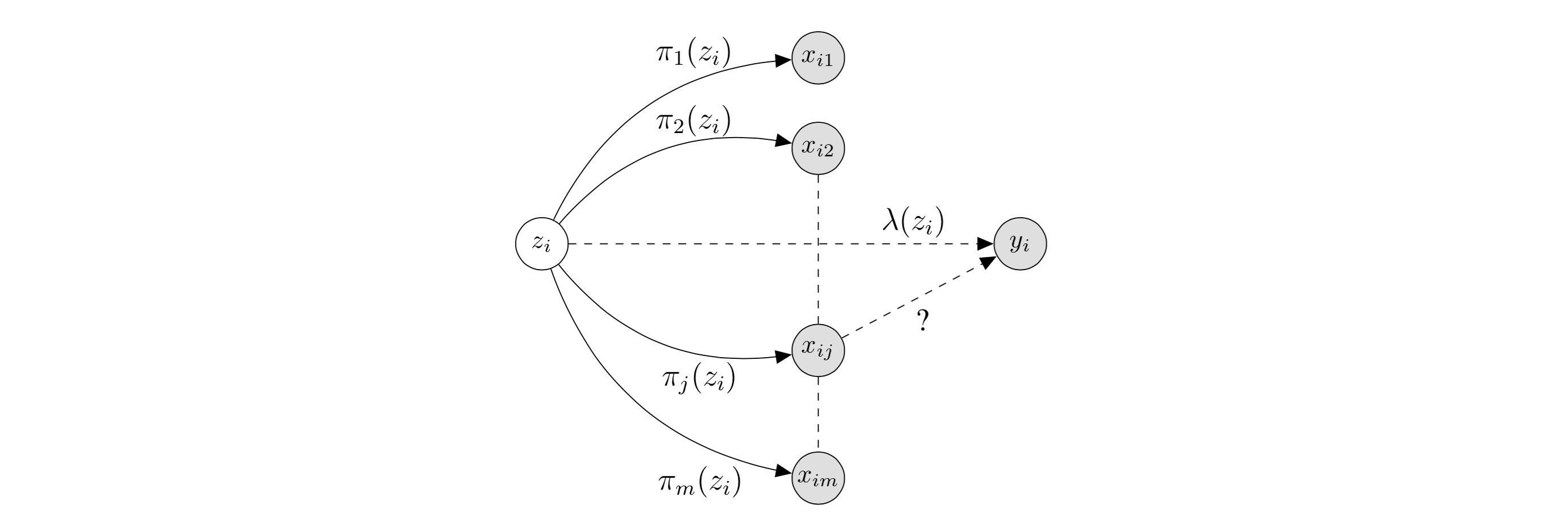
In this diagram, we are testing the causal effect of \(x_{ij}\) on \(y_i\). The latent variable \(z_i\) captures information including population structure (which directly affect the \(x_{ij}\), through \(\pi\)) and non-genetic factors (which directly affect the \(y_i,\) through \(\lambda\)). Thus, by assuming the treatments \(x_{ij}\) only depend on \(z_i\) through \(\pi\), we can remove the confounding effect of \(z_i\) by modeling \(\pi\).
Their full process, known as a “genotype-conditional association test” (GCAT, which are also the four possible nucleotide letters) has two parts:
- Modeling \(\pi_j(z_i)\) to account for the confounding effect of \(z_i\).
- Testing for causality between \(x_{ij}\) and \(y_i\) after accounting for \(\pi_j(z_i)\).
Song et al. use the Hardy-Weinberg Equilibrium to model \(\pi_j(z_i)\). For those of us (like me) who are unfamiliar with biology, the idea is that \(x_{ij}\) takes on values 0, 1, or 2 based on a binomial distribution with some probability; thus, \(\pi_j(z_i)\) is an attempt to model this probability. The authors introduce a method they call “logistic factor analysis” (LFA) as a solution. The full math is a little hairy and is largely based on singular value decompositions and projections which I don’t have the intuition for (check out the paper for more details). The basic model is a matrix decomposition with \(d\) latent factors, so \(\text{logit}(\pi_j(z_i)) = \sum_{k=1}^d h_{ik}a_{kj} = h_i^Ta_j\), and
\[x_{ij} \vert z_i \sim \text{Bin}(2,\text{logit}^{-1}(h_i^Ta_j).\]In this model, the person-specific \(h_i\) and the SNP-specific \(a_j\) are learned using maximum likelihood.
Finally, we would like to test the causal relationship between \(x_{ij}\) and \(y_i\). They test significance by checking if \(\beta_j = 0\) in the following model:
\[y_i = \alpha + \sum_{j=1}^m \beta_jx_{ij} + \lambda_i + \epsilon_i,\]where \(\lambda_i\) is the non-genetic effect and \(\epsilon_i\) is a Gaussian error (both functions of \(z_i\)). However, the authors would prefer to not model \(y_i\), so as to not encode any assumptions about its distribution. The distribution of \(x_{ij}\) is the only one based on a known, scientific phenomenon (the Hardy-Weinberg Equilibrium), so we would like to model as little else as possible. They claim that testing \(\beta_j = 0\) in the above model is equivalent to testing \(b_j = 0\) in:
\[x_{ij} \vert y_i, z_i \sim \text{Bin}(2, \text{logit}^{-1}(a_i + b_jy_i + \text{logit}(\pi_i(z_j))).\]This is known as setting up the problem as an inverse-regression. Finally, they run a likelihood-ratio test to test significance. The paper includes simulation studies that validate the effectiveness of the model.
Final Thoughts
I think the paper does a great job of explaining a novel model, even to someone (like me) who is unfamiliar with biology. There were only a couple of things that confused me: for one, I wasn’t entirely sure why the inverse-regression step was necessary. They claim it’s done to avoid putting a distribution on \(y_i\), but it appears that they’re doing that by including a Gaussian term in the specification of \(y_i\). Another thing I’m not sure about is false discovery rates – it looks like we’re performing the same test for each SNP independently, but I don’t see where we correct for multiple testing (unless it’s somehow incorporated in the \(z_i\) term).
Overall, I highly recommend reading the paper, and I would be excited to see applications in areas outside of genetics.