Training and Inference for Deep Gaussian Processes

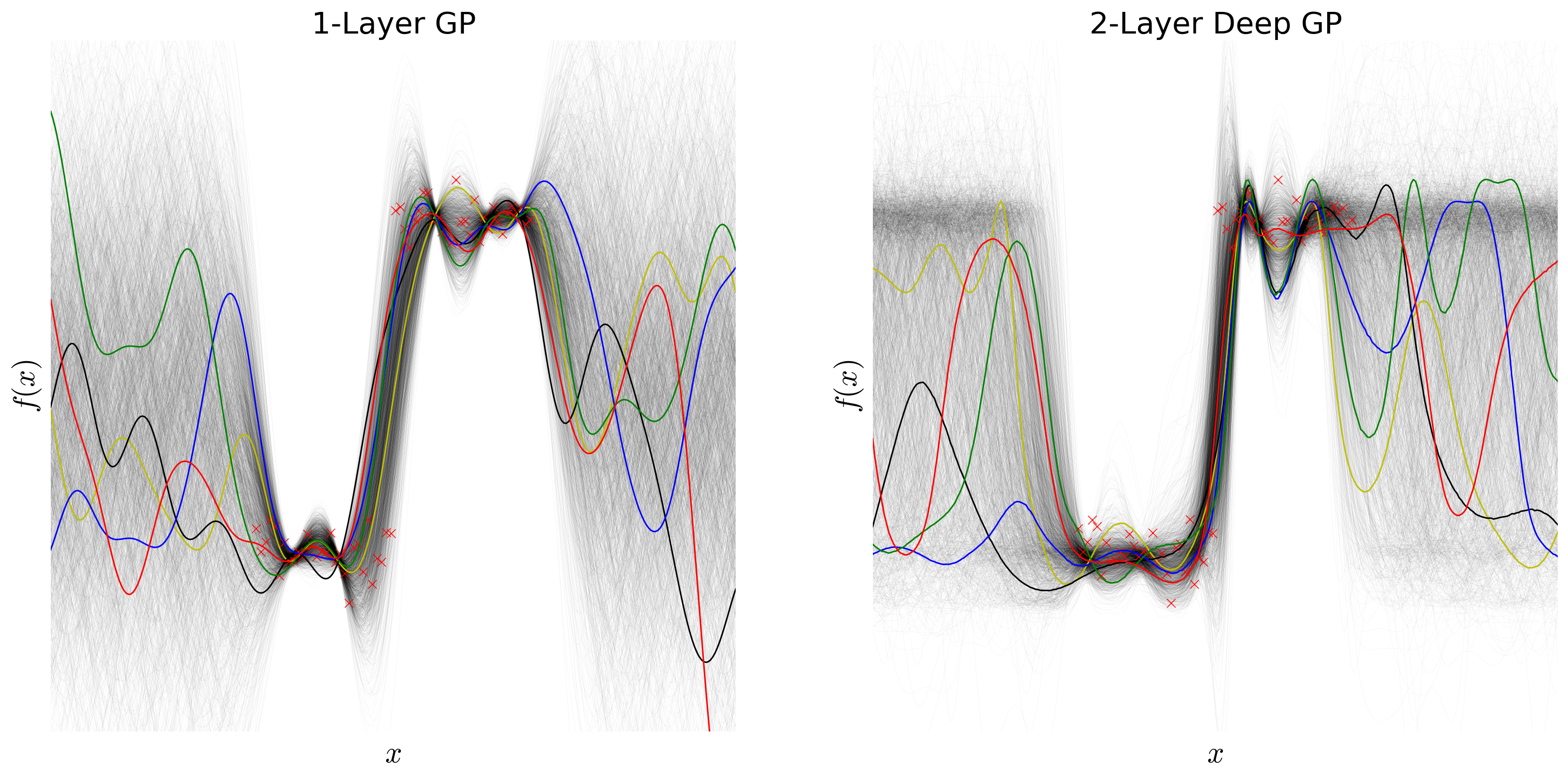
For my undergraduate thesis, advised by Alexander Rush, I explore deep Gaussian processes (deep GPs), a class of models for regression that combines Gaussian processes (GPs) with deep architectures. Exact inference on deep GPs is intractable, and while researchers have proposed variational approximation methods, these models are difficult to implement and do not extend easily to arbitrary kernels. We introduce the Deep Gaussian Process Sampling algorithm (DGPS), which relies on Monte Carlo sampling to circumvent the intractability hurdle and uses pseudo data to ease the computational burden. We build the intuition for this algorithm by defining and discussing GPs and deep GPs, going over their strengths and limitations as models. We then apply the DGPS algorithm to various data sets, and show that deeper architectures are better suited than single-layer GPs to learn complicated functions, especially those involving non-stationary data, although training becomes more difficult due to limitations of local maxima. Throughout, our goal is not only to introduce a novel inference technique, but also to make deep Gaussian processes more accessible to the machine learning community at large. This work would have been impossible without the generous help and support of Finale Doshi-Velez, David Duvenaud, and José Miguel Hernández-Lobato.

My thesis is available here. This led to a workshop paper at the Advances in Approximate Bayesian Inference workshop at NIPS. A blog post and Github tutorial are upcoming.

Slides

The slides below summarize the Deep Gaussian Process Sampling algorithm and highlight our results.